연관토픽
개념
정방행렬 A에 대하여 Ax = λx (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때
상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector)| 구분 | 설명 |
| 고유값 | 행렬 A를 선형변환으로 볼 때, 선형변환 A에 의한 변환결과가 자기 자신의 상수배가 되는 0이 아닌 벡터 |
| 고유벡터 | 행렬 A를 선형변환으로 볼 때, 선형변환 A에 의한 변환 결과에 해당하는 자기 자신의 상수배 값 |
- 행렬 A에 대한 고유값(eigenvalue)은 특성값(characteristic value), 또는 잠정근(latent root)라고도 함
고유값과 고유벡터의 수학적 의미
- 정방행렬 A 에 대해 (1) 식을 만족하는 스칼라 λ와 열벡터 v
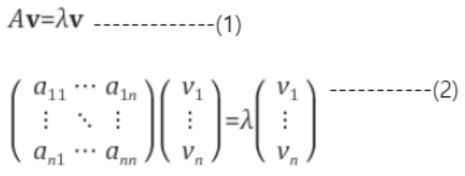
- A가 행렬이고 같은 차원의 벡터 x 에 대해 Ax = λx 를 만족하면, 스칼라 λ는 행렬 A 의 고유값
- 벡터 x 는 스칼라 λ에 대응하는 행렬 A 의 고유벡터
고유값, 고유벡터의 기하학적 의미
행렬의 곱의 결과가 원래 벡터와 "방향"은 같고, "배율"만 상수 λ 만큼만 비례해서 변했다- 정방행렬 A 가 어떤 벡터 v 에 대해 선형변환을 가하는 선형연산자 일 때(즉, 회전변환, 확대/축소변환을 가하는 연산자일 때), 고유벡터의 방향을 유지하며 고유값을 통해 확대/축소변환만 한다고 표현 가능
- 고유벡터는 변화의 축(방향)이 되고, 고유값은 강도 변화의 크기
- 행렬(선형변환) A 의 고유벡터는 선형변환 A 에 의해 방향은 보존되고 스케일(scale)만 변화되는 방향벡터를 나타내고,
- 고유값은 그 고유벡터의 변화되는 스케일 정도를 나타내는 값
모범답안
Reference